A trapezium is a four-sided polygon, also known as a trapezoid in some regions. The defining feature of a trapezium is that it has only one pair of parallel sides. These parallel sides are called the bases of the trapezium. The other two sides, which are not parallel, are referred to as the legs. Knowing how to calculate find the area of a trapezium holds significant value for students and enthusiasts alike. In this blog post, we’ll explore essential steps on how to calculate the area of a trapezium and principles that enable precise calculations of a its area.
Learnerscamp is a dedicated platform designed to assist learners in comprehensively understanding the concept of area. Through practical questions and clear explanations, Learnerscamp provides the essential resources to help you grasp the fundamentals of how to find the area of a trapezium ,how to find the area of a square ,how to find the area of a circle as well as other shapes.
Trapezium
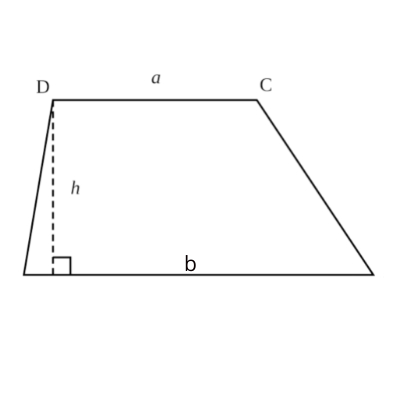
Understanding the Trapezium ( Characteristics of a trapezium )
- Parallel Sides (Bases): A trapezium has two parallel sides, which are called bases. The length of these bases can be different.
- Non-Parallel Sides (Legs): The other two sides are not parallel. They connect the corresponding endpoints of the bases.
- Angles: Trapeziums can have different angle measures. The angles formed by the intersecting sides can vary.
In order to achieve accurate measurements when working with fields related to finding precise surface sizes, it’s essential for individuals to establish a strong foundation before diving into complex calculus. Let’s start by examining the definition of a trapezoid – A quadrilateral shape featuring four sides, two of which are parallel and referred to as bases while the remaining non-parallel links between them are called legs. These connections create various angles based on their lengths in relation to one another.
By mastering this simple concept step-by-step, learners can proceed effectively towards achieving their desired objectives quickly and inconvenience-free. The computational process involves using formulas that tie together different types of inputs such as height and length proportions; these elements form an integral part necessary for successful computations.
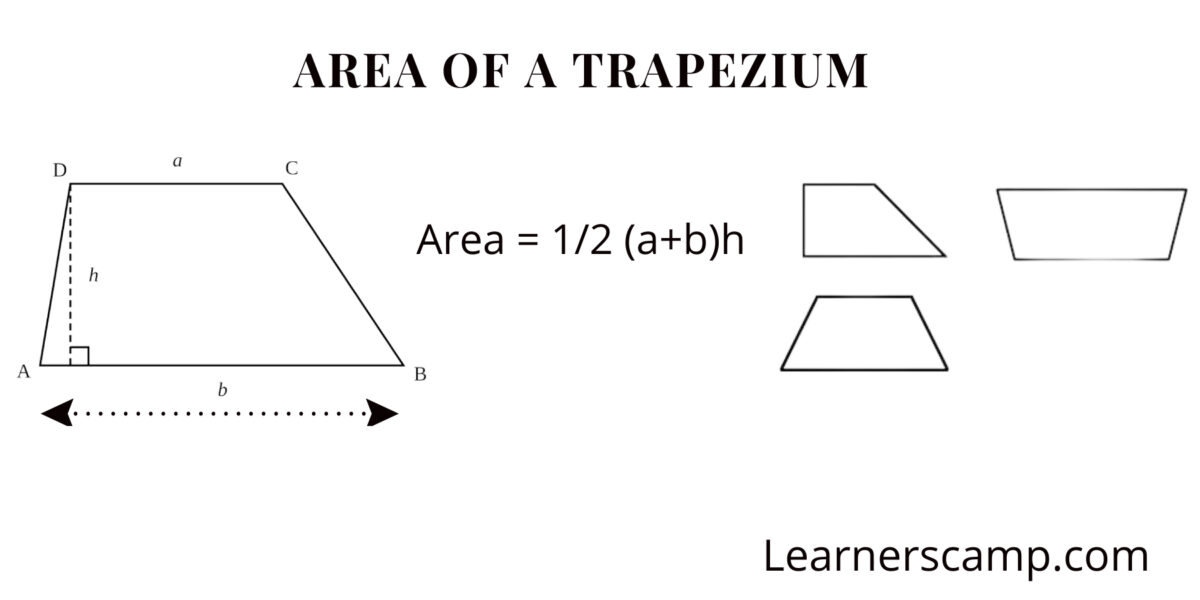
Area of a trapezium
To find the area of a trapezium, we rely on a formula that incorporates the lengths of the bases and the height.
Area of a Trapezium (A)
A=1/2×(a+b)×h
Where:
• a and b are the lengths of the two parallel bases.
• h is the height, the perpendicular distance between the bases.
Step-by-Step Guide:
Procedure in Detail: Firstly, let us divide the procedure into digestible stages:
- Determine the Height along with Bases: Start by determining the height (h) and the two parallel bases (a and b) of the trapezium. The height is the distance between the bases measured perpendicularly.
- Enter Values into the Formula: Enter a, b, and h’s values into the area equation.
- Perform the Calculation: Execute the calculations systematically, following the order of operations. Keep in mind that the formula involves addition, multiplication, and division.
- Finalize the Result: The result obtained represents the area of the trapezium. Ensure it is expressed in square units, matching the unit of length used for the bases and height.
Examples
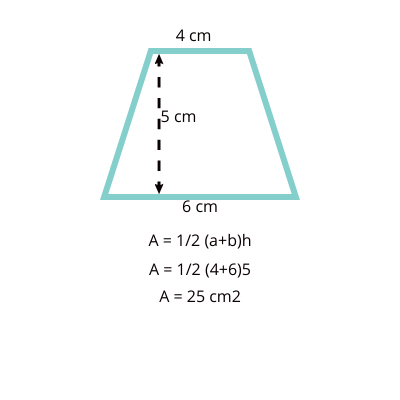
Real-world Applications
Understanding how to find the area of a trapezium extends beyond textbook exercises:
• Architecture: Architects use trapezium area calculations when designing buildings with irregular floor plans, helping optimize space.
• Surveying: Surveyors apply trapezium area formulas in land measurements, particularly when dealing with uneven terrains.
As we explain the steps on how to find the area of a trapezium, the formula A=1/2×(a+b)×h becomes our guiding light. In essence, mastering the calculation of the area involves a clear understanding of the bases a and b and the height ℎ.
Remember that the area of a trapezium is within your mathematical reach the next time you come across one in your geometry problems or practical applications.
