Two Dimentional shapes

Understanding two-dimensional shapes is fundamental in geometry. In this guide, we'll explore common two-dimensional shapes, their properties, and how to identify them. Remember that these shapes exist in two dimensions - length and width.

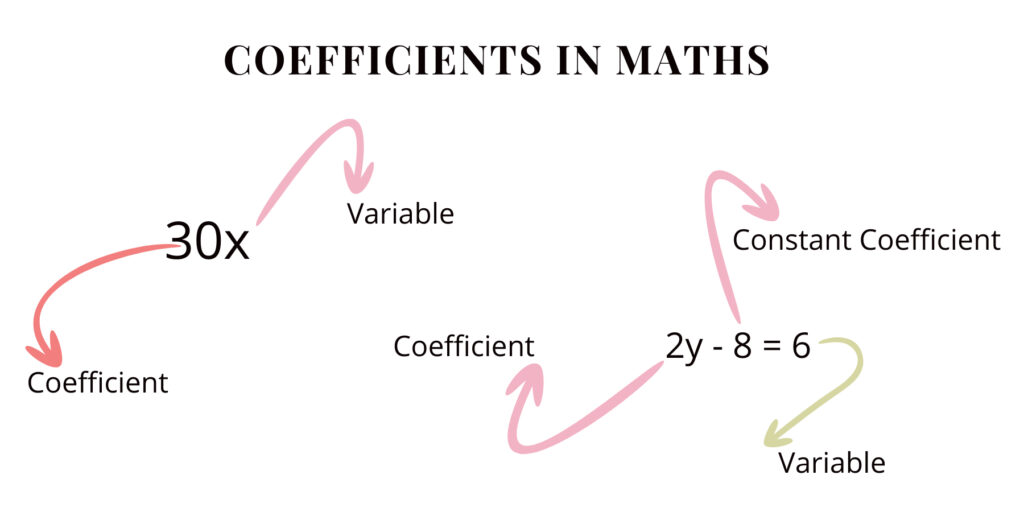
With a focus on mathematical calculations, Learnerscamp provides dynamic tutorials, real-world applications, and problem-solving scenarios that empower students to grasp mathematical concepts such as area of shapes like rectangles, squares , circles , trapeziums among others with ease. Our adaptive learning algorithms ensure personalized learning paths, allowing students to progress at their own pace while receiving instant feedback to reinforce their understanding.

Two-Dimensional Shapes

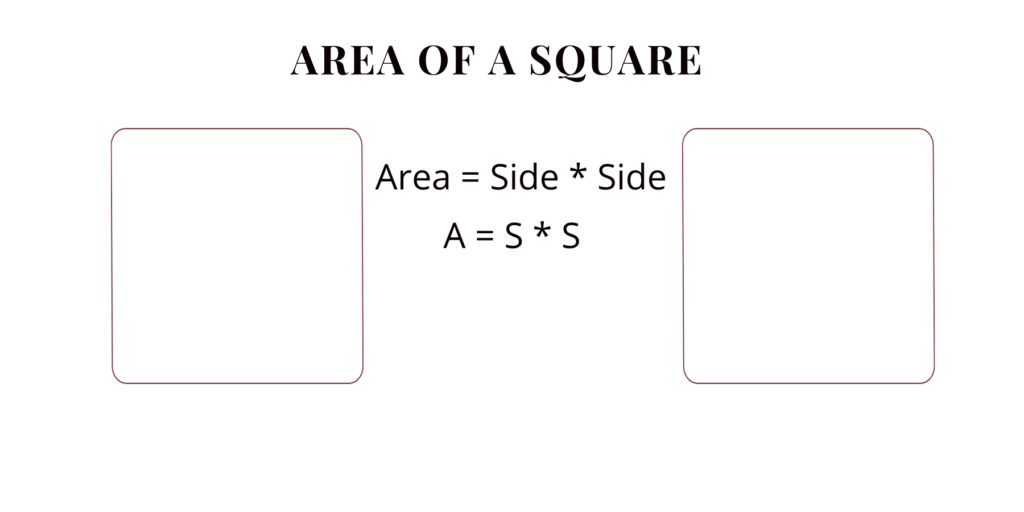
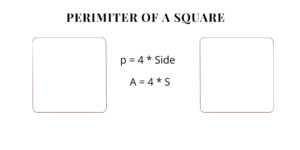
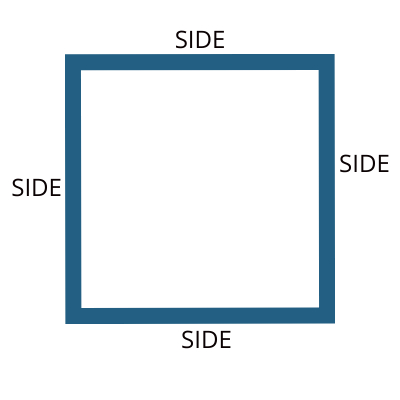
1. Square

A square is a four-sided polygon with all sides of equal length and all angles equal to 90 degrees.

Identification: Look for a shape with four equal sides and right-angle corners.

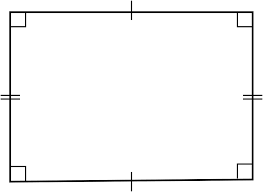
2. Rectangle

A rectangle is a four-sided polygon with opposite sides of equal length and all angles equal to 90 degrees.

Identification: Similar to a square but with opposite sides of different lengths.

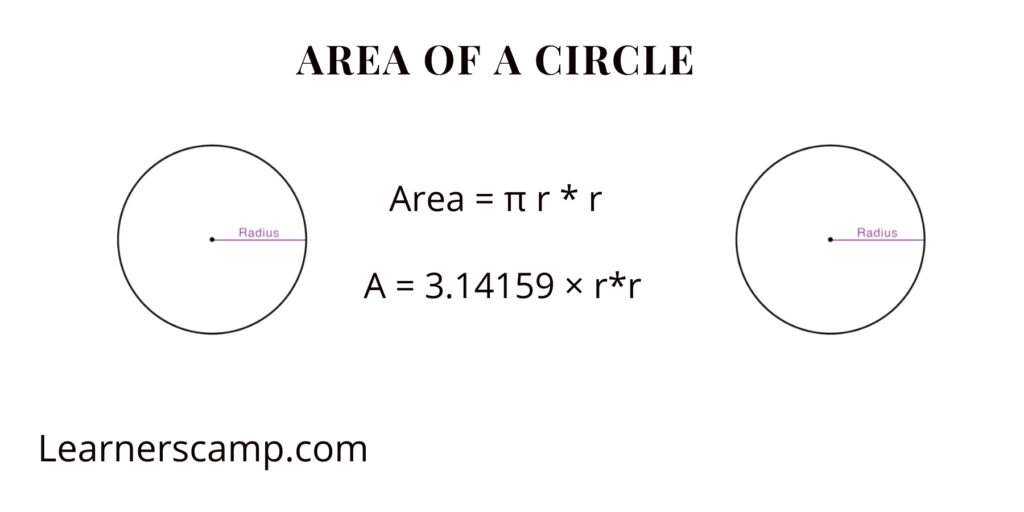
3. Circle

A circle is a round shape with all points on its boundary equidistant from its center creating a symmetrical and round form.

Identification: Look for a perfectly round shape.

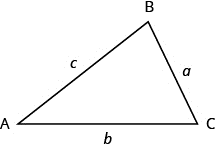
4. Triangle

A triangle is a three-sided polygon with three angles and three sides coming in various types such as equilateral (all sides equal), isosceles (two sides equal), and scalene (no sides equal).

Identification: Observe a shape with three sides and three corners.

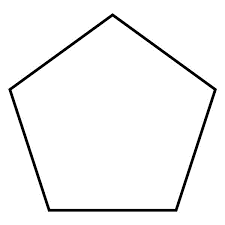
5. Pentagon

A pentagon is a five-sided polygon.

Identification: Count the number of sides; a pentagon has five.

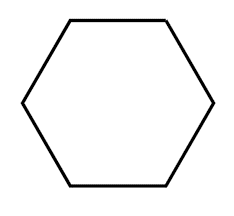
6. Hexagon:

A hexagon is a six-sided polygon with six angles and six straight sides, featuring a hexagonal symmetry that is commonly observed in nature and man-made structures.

Identification: Count the number of sides; a hexagon has six.

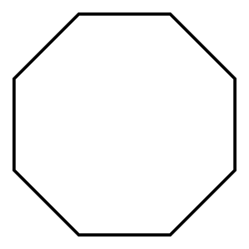
7. Octagon

An octagon is an eight-sided polygon with eight angles and eight straight sides, known for its regularity and often used in the design of stop signs and other symbols.

Identification: Count the number of sides; an octagon has eight.

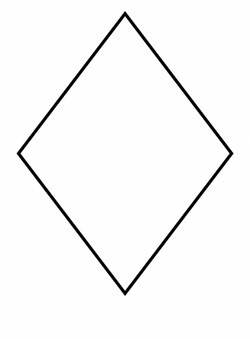
8. Rhombus

A rhombus is a four-sided polygon with all sides of equal length, but angles are not necessarily 90 degrees, creating a tilted and diamond-shaped figure.

Identification: Look for a shape with equal sides but not necessarily right angles.

9. Parallelogram

A parallelogram is a four-sided polygon with opposite sides that are both equal in length and opposite angles that are equal.

Identification: Observe a shape with opposite sides and angles that are equal.

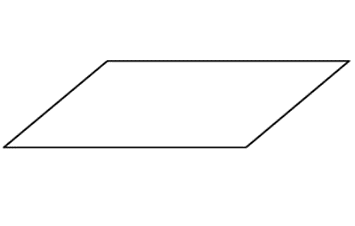
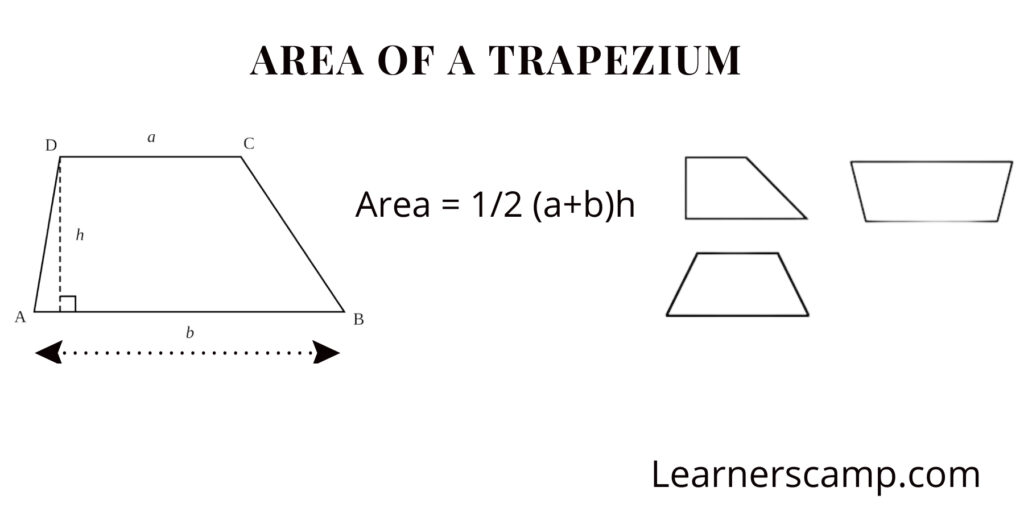
10. Trapezoid

A trapezoid is a quadrilateral with one pair of parallel sides distinguishing it from other quadrilaterals by its asymmetry.

Identification: Look for a shape with one set of parallel sides./p>

Key Characteristics

Flatness

Two-dimensional shapes exist in a plane and are flat, lacking volume or depth.

Vertices and Edges

Vertices are points where the edges of a shape meet. Edges are the lines that form the boundaries of the shape.

Closed Figures

Two-dimensional shapes are often closed figures, meaning they have distinct boundaries that enclose a space.

Common Two-Dimensional Shapes

1. Triangles

Three-sided polygons with varying side lengths and angles. Classified by sides and angles into types such as equilateral, isosceles, and scalene.

2. Quadrilaterals

Four-sided polygons with diverse characteristics. Includes rectangles, squares, parallelograms, and rhombuses.

3. Circles

Perfectly round shapes defined by a central point (center) and a consistent radius.

4. Polygons

Closed shapes with multiple straight sides. Regular polygons have equal sides and angles.

5. Irregular Shapes

Shapes that do not conform to standard classifications, often with varying side lengths and angles.

These two-dimensional shapes form the foundation of geometry. Practice identifying them to enhance your understanding of their properties and relationships. Geometry becomes more accessible when you can recognize and work with these fundamental