Circles, with their perfect symmetry and endless applications in geometry, engineering, and everyday life, hold a unique place in mathematics. One fundamental property of a circle is its perimeter, which is the boundary that encloses the circle. Understanding how to find the perimeter of a circle is essential not only for academic pursuits but also for practical applications. In this blog, we will help you understand how to find the perimeter of a circle/calculate the circumference of a circle, and explore various methods to master this fundamental concept.
Leanerscamp has come in handy to help many students understand different mathematical concepts including how to find the perimeter of a circle. With the help of well-structured study guides, revision questions, and detailed reports, Learnerscamp is well-known to generally help students prepare. Visit and find out how helpful they can be.
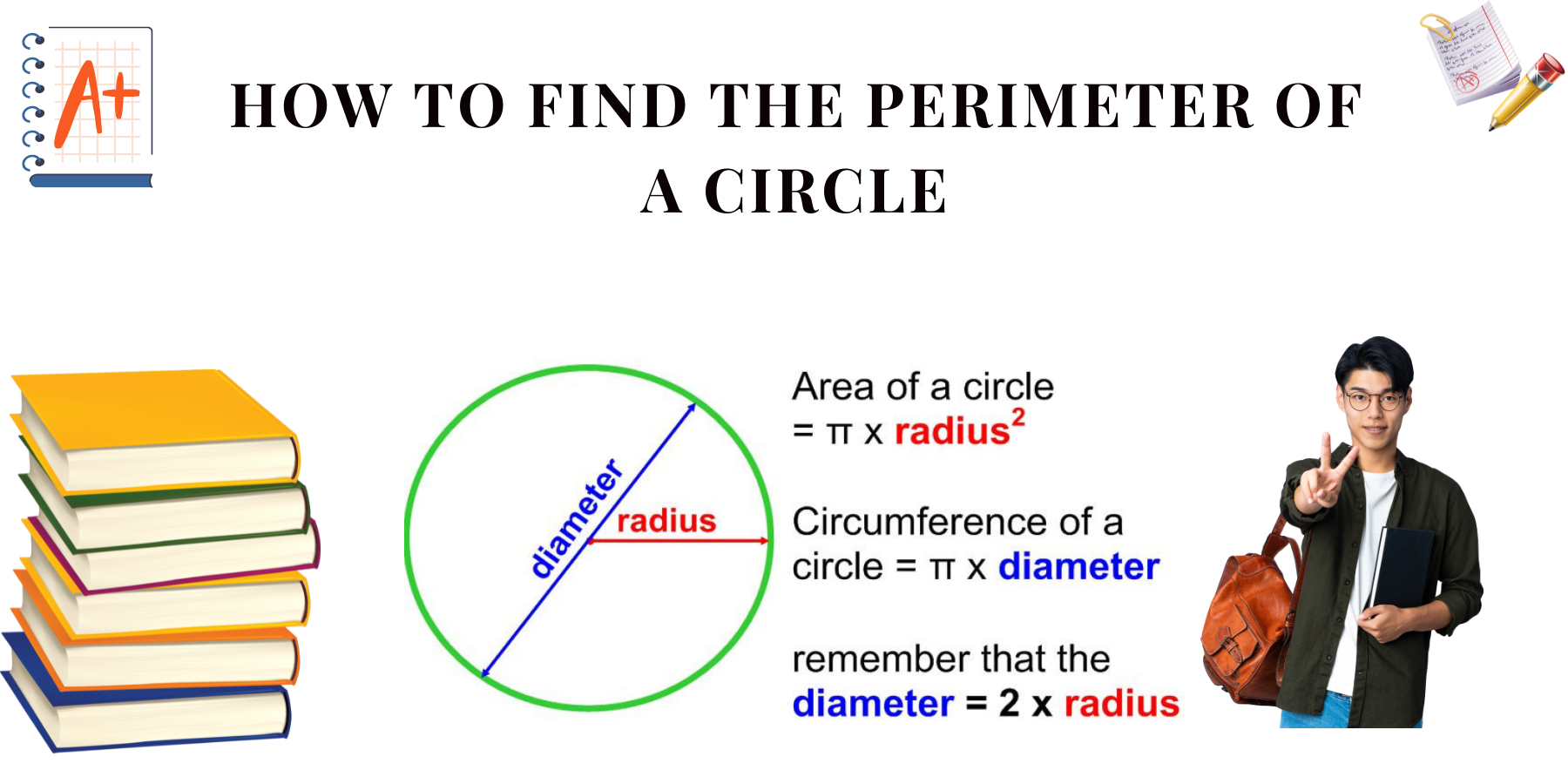
The perimeter of a circle is often referred to as its circumference. It is the distance around the outer boundary of the circle. Unlike other geometric shapes, the perimeter of a circle is not simply the sum of its sides but is calculated using its radius or diameter.
How to find the perimeter of a circle
The Radius Approach:
The most common method to find the perimeter of a circle is by using the circumference formula. The circumference (C) of a circle is given by the formula:
C = 2πr
Where:
C is the circumference,
π is a mathematical constant approximately equal to 3.14159
r is the radius of the circle.
This formula encapsulates the relationship between the circumference and the radius of a circle. By simply plugging in the value of the radius into the formula, one can easily calculate the perimeter of the circle.
Example
Let’s consider an example to illustrate the application of the circumference formula. Suppose we have a circle with a radius of 5 units .To find the perimeter (circumference) of this circle, we can substitute the value of the radius into the formula:
Circumference = 2πr
C = 2 × 3.14159 × 5
C = 31.4159 units
Thus, the perimeter of the circle is 31.4159 units.
The Diameter Approach
Another approach to finding the perimeter of a circle involves using its diameter. The diameter of a circle is the distance across the circle through its center. It is twice the length of the radius ( d=2r). Therefore, an alternative formula to find the circumference of a circle is C = πd. This formula utilizes the diameter instead of the radius to calculate the perimeter of the circle.
Choosing the Right Method
When finding the perimeter of a circle, it is essential to choose the appropriate method based on the given information. If the radius is provided or easily determined, using the circumference formula C = 2πr is straightforward and efficient. However, if the diameter is given instead, employing the formula C = πd would be more appropriate.
With this, you should be able to calculate the circumference/perimeter of any circle. For more, visit Learnerscamp today, as it engages you through a series of mathematical concepts that will help you gain a deeper understanding of whichever math topic you would wish to learn