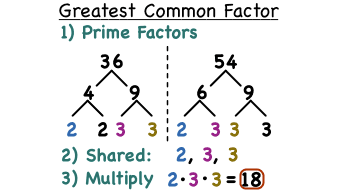
In the vast landscape of mathematics, the concept of the Greatest Common Divisor (GCD) serves as a cornerstone, offering invaluable insights into the relationships between numbers. Thus, the GCD, representing the largest integer that divides two or more numbers without leaving a remainder, holds significant relevance in various mathematical contexts. Hence, by employing a systematic approach that focuses on utilizing factors to find the greatest common divisor, individuals can efficiently determine the GCD of a set of numbers. As such, this comprehensive exploration delves into the intricacies of GCD calculation, unraveling its nuances through practical illustrations and problem-solving strategies. Therefore, by the end of this journey, you will emerge equipped with the knowledge and skills to navigate GCD calculation with confidence and precision.
Before we delve deeper into exploring integers and number lines, I would like to remind you as a learner that LearnersCamp provides additional insights into these disparities. Additionally, LearnersCamp has grown to become a valuable platform for learners seeking to deepen their understanding of mathematical concepts. Moreover, it has a user-friendly interface and a vast array of educational materials, including articles, tutorials, and interactive quizzes; LearnersCamp offers comprehensive guidance on such topics. Hence, by visiting LearnersCamp, learners can access clear explanations, practical examples, and engaging exercises to solidify their grasp of these fundamental mathematical principles.
Understanding utilization of Factors to Find the Greatest Common Divisor
Before delving into the mechanics of GCD calculation, it’s essential to grasp the fundamental principles underlying this concept. The GCD serves as a measure of the highest common factor shared by two or more numbers, thus, providing a basis for understanding their divisibility relationships. Eventually, by determining the GCD, mathematicians can unveil patterns, identify common factors, and unravel the mathematical intricacies used in utilizing factors to find the greatest common divisor.
Explore the process of utilizing factors to find the greatest common divisor.
- Finding GCD by Listing Factors:
The process of finding the GCD begins, firstly, with listing the factors of each number within the set. Factors, representing the numbers that divide a given number without leaving a remainder, serve as building blocks in GCD calculation. That is, by systematically listing the factors of each number, individuals lay the groundwork for identifying common factors and determining the GCD.
- List Factors:
First, begin by meticulously listing all the factors of each number within the set. This step involves systematically identifying the numbers that evenly divide each given number, encompassing both the positive and negative factors. That is, by methodically listing the factors, individuals create a comprehensive inventory that serves as the foundation for subsequent GCD calculations. - Identify Common Factors:
Once the factors of each number have been listed, the focus shifts to identifying the common factors shared among all the numbers within the set. Common factors represent the pivotal elements that contribute to the GCD, as they are the numbers that uniformly divide each number without leaving a remainder. In any case, by scrutinizing the lists of factors, individuals can pinpoint these common factors, laying the groundwork for determining the GCD. - Choose the Greatest Common Divisor:
Finally, having identified the common factors shared among the numbers within the set, select the greatest common factor as the GCD. This process entails scrutinizing the list of common factors and identifying the largest integer that uniformly divides all the numbers without leaving a remainder. Emphatically, by choosing the greatest common factor as the GCD, individuals pinpoint the highest common divisor shared by the numbers within the set, providing a definitive measure of their mathematical relationship.
Solving Problems Involving GCD Calculation:
To solidify comprehension and proficiency in GCD calculation, let’s embark on a journey to tackle a series of word problems.
- Problem 1:
Find the GCD of the numbers 18, 24, and 36.
Solution:
- List the factors of each number:
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Identify common factors: 1, 2, 3, 6
- Choose the greatest common factor: GCD(18, 24, 36) = 6
Let’s apply the same systematic approach to tackle another word problem.
- Problem 2:
Determine the GCD of 60, 72, and 96.
Solution:
- List the factors of each number:
- Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
- Identify common factors: 1, 2, 3, 6, 12
- Choose the greatest common factor: GCD(60, 72, 96) = 12
Conclusion:
In conclusion, the process of finding the GCD using factors offers a systematic and efficient approach to unraveling the mathematical relationships between numbers. Thus, meticulously listing factors, identifying common ones, and selecting the greatest common factor as the GCD, individuals gain valuable insights into the mathematical properties of sets of numbers. Moreover, armed with this knowledge and guided by practical illustrations and problem-solving strategies, learners can navigate GCD calculation with confidence and precision, unlocking mathematical insights and empowering themselves to tackle complex problems with ease. As such, you continue your mathematical journey, remembering to leverage the power of GCD calculation, utilizing factors as your guiding light in exploring the fascinating realm of number theory.