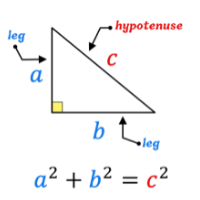
Most students often ask the question what is the Pythagoras theorem The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Pythagoras Theorem Expression
Mathematically, Pythagorean Theorem can be expressed as:
c² = a² + b²
here :
c represents the length of the hypotenuse,
a and b represent the lengths of the other two sides.
This Pythagoras Theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery, although the principle was known to Babylonian mathematicians over a millennium earlier. The Pythagorean Theorem is widely used in various fields, including geometry, physics, engineering, and computer science.
What is the Pythagorean theorem rule?
It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Click here to see a sample question touching on the Pythagoras formulae and how its applied in a mathematical computation
The Converse of the Pythagorean Theorem
The Converse of the Pythagorean Theorem is a statement that explores the relationship between the sides of a triangle and determines whether the triangle is a right triangle
The converse of the Pythagoras theorem states that,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Converse of Pythagoras Theorem Proof
For a triangle with the length of its sides a, b, if c2 = a2 + b2, we need to prove that the triangle is right-angled.
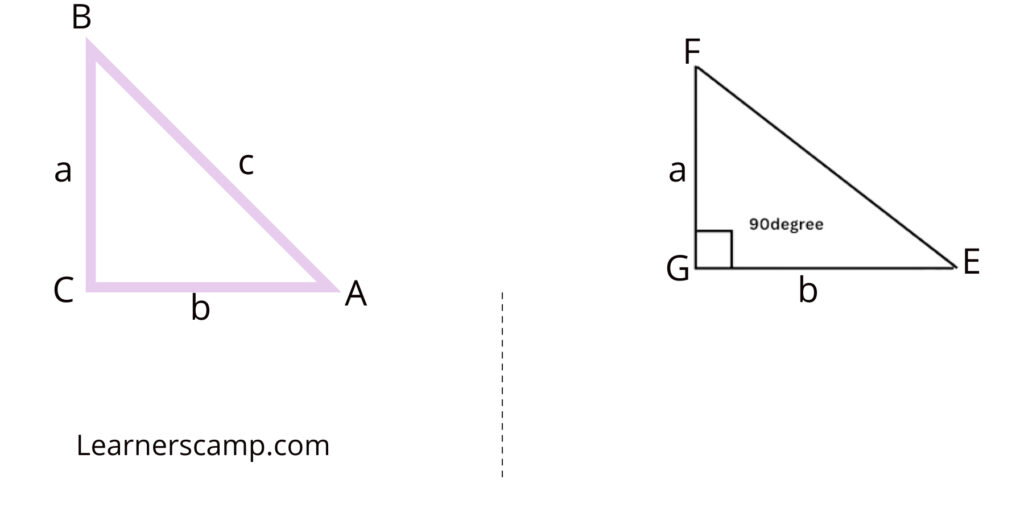
We assume that it satisfies c2 = a2 + b2, and by looking into the diagram, we can tell that ∠C = 90°, but to prove it, we require another triangle △EGF, such as AC = EG = b and BC = FG = a.
In △EGF, by Pythagoras Theorem:
⇒ EF2 = EG2 + FG22 = b2 + a2 ⇢ (1)
In △ABC, by Pythagoras Theorem:
⇒ AB2 = AC2 + BC2 = b2 + a2 ⇢ (2)
From equation (1) and (2), we have;
⇒ EF2 = AB2
EF = AB
△ ACB ≅ △EGF (By SSS postulate)
⇒ ∠G is right angle
Thus, △EGF is a right triangle. Hence, we can say that the converse of the Pythagorean theorem also holds.




