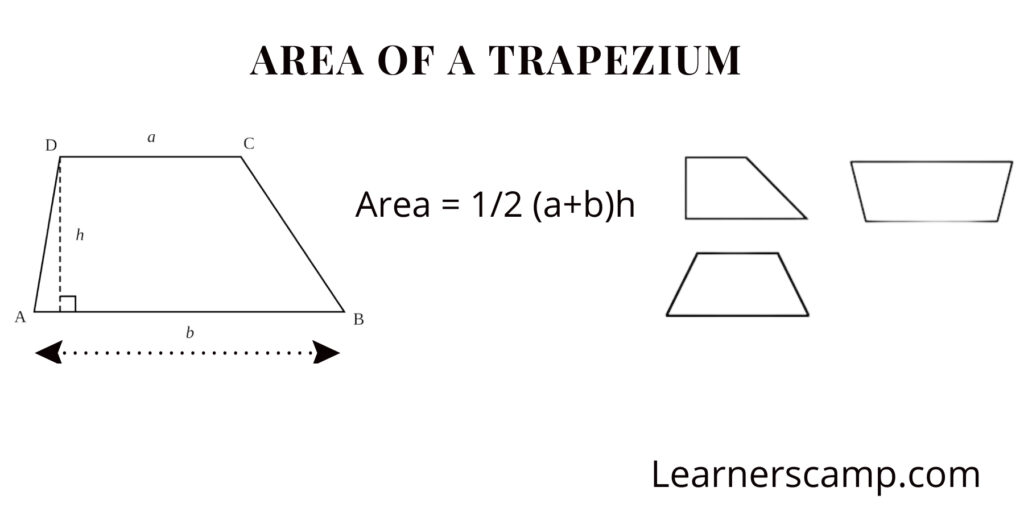
Area
Area refers to the measure of the amount of space within the boundary of a two-dimensional shape or region. It is usually expressed in square units, such as square meters, square centimeters, square inches, etc. The concept of area is fundamental in geometry and is used to quantify the size of shapes like squares rectangles, triangles, circles, and more complex figures.
Learnerscamp assists students in understanding geometric equations by providing educational resources such as how to find the area of a circle, how to find the area of a square ,how to find the area of a rectangle interactive lessons, and practice problems. Additionally, learners can benefit from personalized feedback and progress tracking, enhancing their overall comprehension of geometry.
The formula for calculating the area depends on the specific shape. Here are the formulas for some common shapes:
Formula for Area of a rectangle
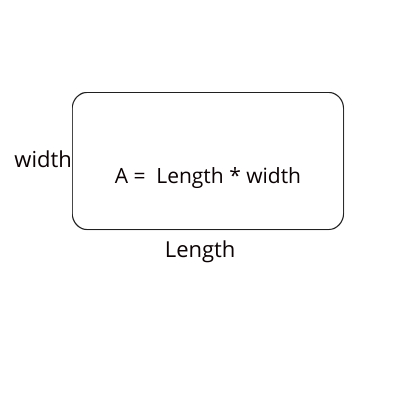
Area = Length * Width ( where "length" and "width" are the dimensions of the rectangle.)
A rectangle is a geometric shape that is characterized by having four sides and four right angles (90-degree angles). The opposite sides of a rectangle are equal in length, and all interior angles are right angles. In other words, a rectangle is a type of parallelogram with four right angles.
Key properties of a rectangle
- Four sides: A rectangle has four straight sides.
- Opposite sides are equal in length: The pairs of opposite sides in a rectangle are of equal length.
- Four right angles: All interior angles of a rectangle measure 90 degrees.
- Diagonals are equal: The diagonals of a rectangle are of equal length and bisect each other.
Examples of rectangular shapes include doors, windows, book covers, and many other objects with four straight sides and right angles.
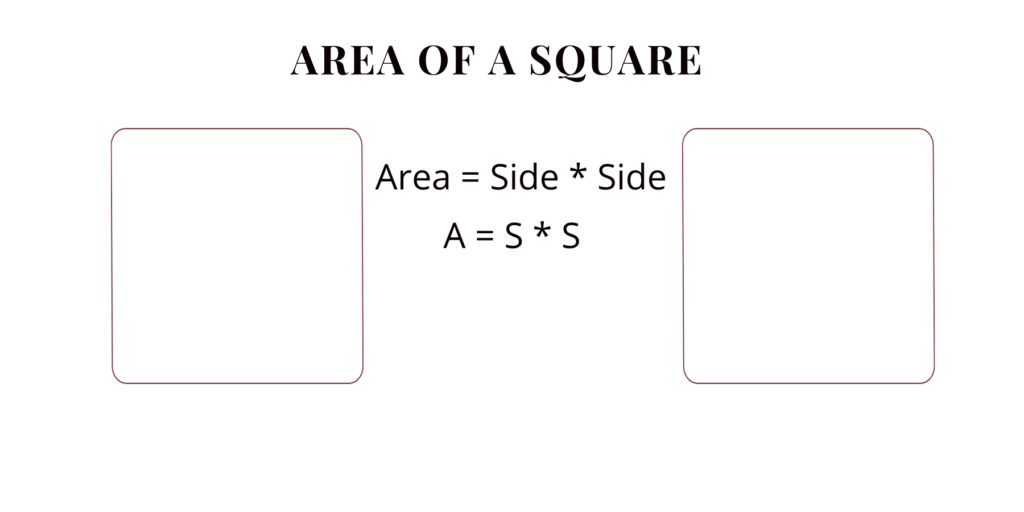
Formula for Area of a Square
Area = Length * Length | Side * Side (where "side " is the length of one side of the square.)
A square is a special type of polygon, which is a two-dimensional shape with four straight sides of equal length and four right angles (90-degree angles) between adjacent sides. Each corner of a square is a right angle, and all the sides are of equal length.
Key properties of a Square
- Equal sides: All four sides of a square are of the same length.
- Right angles: All four interior angles are 90 degrees.
- Diagonals: The diagonals of a square bisect each other at right angles, and they are of equal length.
- Symmetry: A square has fourfold rotational symmetry, meaning that you can rotate it by 90 degrees, and it looks the same.
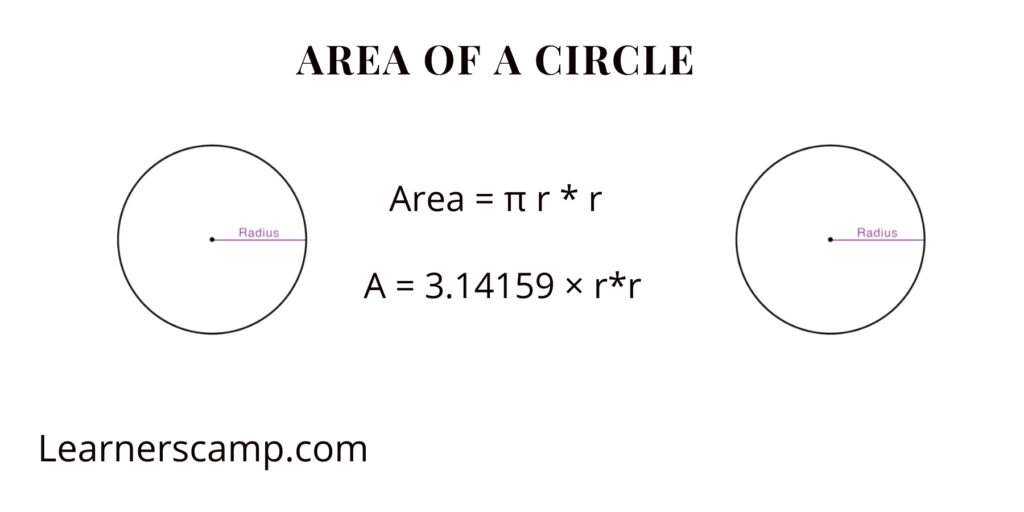
Formula for Area of a Circle
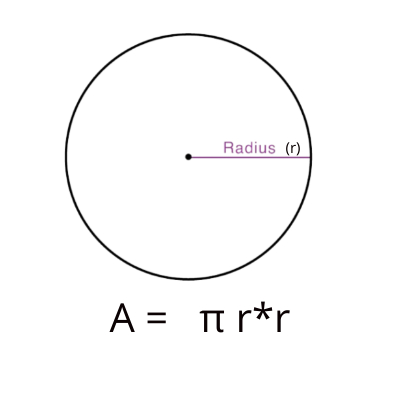
Area = π * radius * radius (where "π" is 3.142 )
π is defined as the ratio of the circumference to the diameter of any circle
A square is a two-dimensional geometric shape that consists of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is called the radius. The longest chord of a circle, which passes through the center, is called the diameter, and it is twice the length of the radius.
Terms associated with Circles
- Center: The fixed point in the plane from which all points on the circle are equidistant.
- Radius: The distance from the center of the circle to any point on the circle. Denoted by "r."
- Diameter: The longest chord of the circle, which passes through the center. The diameter is twice the length of the radius. Denoted by "d."
- Chord: A line segment connecting two points on the circle.
- Circumference: The total distance around the circle
- Area: The measure of the space enclosed by the circle.
More on LearnersCamp
Learnerscamp is a dedicated platform designed to assist learners in comprehensively understanding different mathematical concepts