Finding the area of a parallelogram unveils insights into its structure and dimensions. In addition, this offers a valuable skill for students and enthusiasts alike. In the realm of geometry, parallelograms present themselves as fascinating quadrilaterals with unique properties. As a result, this blog embarks on a journey to understand the principles and methods of how to find the area of a parallelogram, exploring its significance and real-world applications.
Leanerscamp is a dedicated platform designed to assist students learn different maths topics with the help of our rich study resources. Additionally, learners can benefit from personalized feedback and progress tracking, enhancing their overall studies in any maths topic of their choice.
How to Find the Area of a Parallelogram Made Simple
Ease the process of calculating the area of a triangle with this comprehensive guide. Get to learn of step-by-step methods and key principles for accurate geometric calculations. For instance, Learnerscamp is a dedicated platform designed to assist learners in comprehensively understanding the concept of area. Additionally,through practical questions and clear explanation Learnerscamp provides the essential resources to help you grasp the fundamentals of how to find the area of a trapezium ,how to find the area of a square ,how to find the area of a circle as well as other shapes.
Discover the secrets of finding the area of a parallelogram with this comprehensive guide. Unveil step-by-step methods and gain insights into the geometric properties of parallelograms.
How to Find the Area of a Parallelogram
Understanding the Parallelogram:
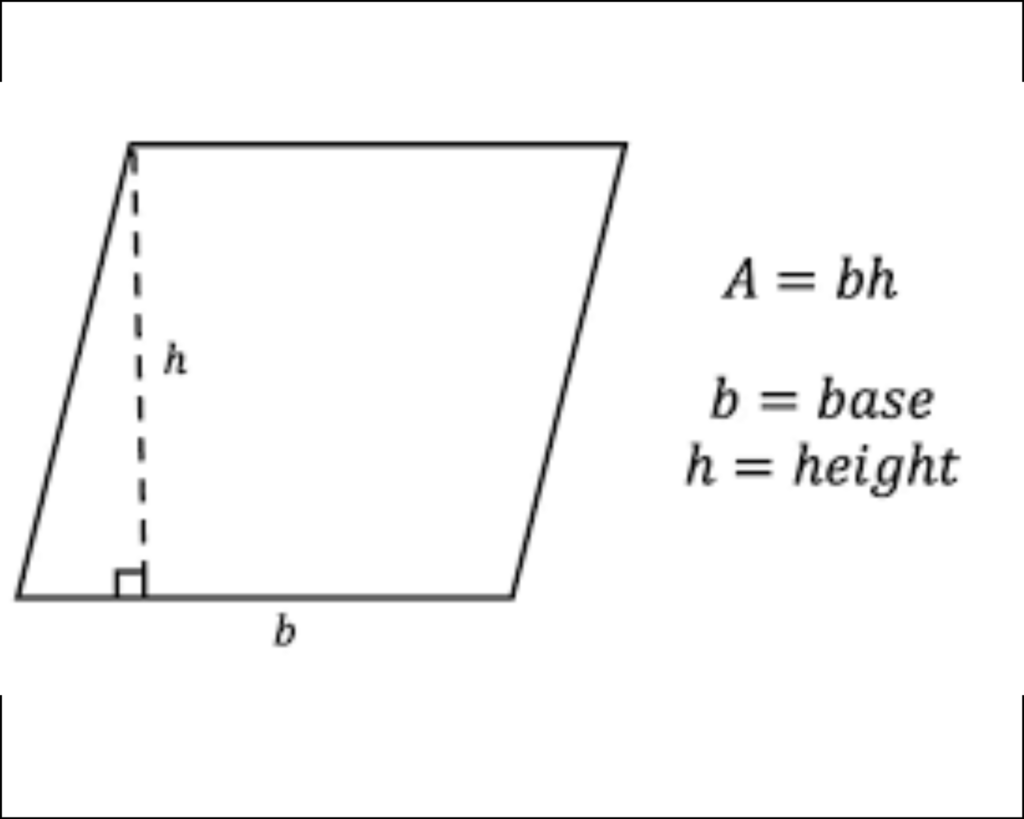
Before delving into calculations, let’s grasp the essence of a parallelogram. A parallelogram is a four-sided polygon with opposite sides parallel and equal in length. Therefore, to find its area, we utilize a simple formula that incorporates the base and height of the parallelogram.
Key Formula: Area of a Parallelogram (A)
Area = b x h
Where:
– b is the length of the base of the parallelogram.
– h is the height, the perpendicular distance between the base and its opposite side.
Step-by-Step Guide:
Let’s break down the process into simple steps:
1. Identify the Base and Height:
Begin by identifying the length of the base ( b ) and the height ( h ) of the parallelogram. The height is the perpendicular distance between the base and its opposite side.
2. Plug Values into the Formula:
Substitute the values of b and h into the area formula.
3. Perform the Calculation:
Execute the multiplication operation to find the area.
4. Finalize the Result:
The result obtained represents the area of the parallelogram. Afterwards, express it in square units, matching the unit of length used for the base and height.
Real-world Applications:
Understanding how to find the area of a parallelogram extends beyond mathematical exercises:
– Architecture:
Architects use parallelogram area calculations when designing floor plans and determining usable space.
– Land Surveying:
Surveyors apply parallelogram area formulas in land measurements, especially when dealing with irregularly shaped plots.
Example:
Let’s find the area of a parallelogram with a base of 8 units and a height of 5 units.
Given:
– Base (b): 8 units
– Height (h): 5 units
Using the formula:
A = b x h
The area = 8 x 5
= 40
Therefore, the area of the parallelogram is 40 square units.
For the purpose of navigating the geometric terrain, the formula A = b x h becomes our compass, guiding us in finding the area of a parallelogram. As a matter of fact, mastery of this calculation hinges on a clear understanding of the base b and the height h.
So, the next time you encounter a parallelogram in your geometric explorations or real-world applications, remember that finding the area of a parallelogram is within your grasp through simple multiplication.
In conclusion, this comprehensive guide equips you with the knowledge to navigate the intricacies of parallelograms, making geometric calculations an accessible and valuable skill. Happy exploring!




