What is a plane in geometry

What is a plane in geometry ? In the realm of geometry, planes serve as fundamental geometric elements essential for understanding spatial relationships and shapes in three-dimensional space. This comprehensive review aims to elucidate the concept of planes in geometry, elucidating their definition, properties, and practical applications.

 LearnersCamp has emerged as a highly effective tool in aiding students in their journey to understand and master geometry. By combining interactive elements, such as coefficients in mathematic, personalized learning paths, and a collaborative community, the platform has successfully transformed the way students approach and conquer this challenging mathematical discipline.

Definition and Characteristics:

A plane in geometry is a flat, two-dimensional surface that extends infinitely in all directions. It is defined by a collection of points that lie in the same plane and can be visualized as a perfectly flat surface with no thickness or curvature. Some key characteristics of planes include:

• Infinite Extension: A plane extends indefinitely in all directions, encompassing an infinite number of points.
• Flatness: Unlike curved surfaces, a plane remains perfectly flat and does not exhibit any curvature.
• Uniformity: All points on a plane lie at an equal distance from each other, maintaining a consistent arrangement across the surface.

Equations and Representations:

Planes in geometry can be defined and represented in various ways, including:

• Cartesian Equation:  A plane can be defined by an equation in the form ax + by + cz + d = 0, where A, B, and C are constants representing the coefficients of the P, N, and Q variables, respectively, and D is a constant representing the distance of the plane from the origin along the direction of the plane’s normal vector.

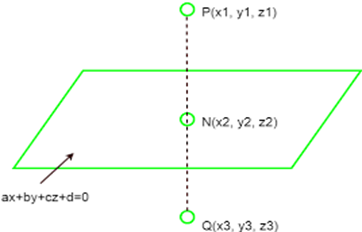
• Vector Equation: A plane can also be described using a vector equation, which specifies a point on the plane and a vector orthogonal to the plane’s surface.
• Parametric Equations: Parametric equations offer another method of defining a plane, expressing the coordinates of points on the plane in terms of two independent parameters.

Applications in Geometry and Engineering:

The concept of planes finds widespread applications in various fields, including architecture, engineering, computer graphics, and physics. In architecture and engineering, planes are used to represent surfaces such as walls, floors, and ceilings, facilitating the design and construction of structures. In computer graphics, planes serve as the foundation for rendering three-dimensional scenes onto two-dimensional screens, allowing for realistic simulations and visualizations.

Properties and Relationships:

Planes exhibit several important properties and relationships in geometry, including:

1. Parallelism: Two planes are parallel if they do not intersect and have the same slope or direction.
2. Intersection: When two planes intersect, they form a line known as the intersection line.
3. Angle between Planes: The angle between two planes is determine by the angle between their normal vectors.
4. Distance from a Point to a Plane: The distance from a point to a plane is the perpendicular distance from the point to the plane’s surface.

Applications in Geometry and Beyond:

The concept of planes finds widespread applications across various fields, including:

1. Geometry: Planes serve as foundational elements in geometric proofs, constructions, and spatial reasoning.
2. Engineering and Architecture: Engineers and architects use planes to represent surfaces, such as floors, walls, and ceilings, in building designs and structural analysis.
3. Computer Graphics: In computer graphics and modeling, you can use plane represent surfaces in three-dimensional rendering and animation.

 Intersection with Lines and Planes:

A line can intersect a plane in various ways:

1. It can intersect the plane at a single point.
2. It can lie entirely in the plane.
3. It can be parallel to the plane and never intersect it.
4. Two planes can intersect to form a line if they are not parallel.

Distance from a Point to a Plane:

The distance between a point and a plane is the length of the perpendicular segment from the point to the plane. one can calculate using the formula:

Distance = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)

Types of Planes:

1. Horizontal Plane: Parallel to the horizon, perpendicular to the vertical direction.
2. Vertical Plane: Perpendicular to the ground, parallel to the vertical direction.
3. Oblique Plane: Neither horizontal nor vertical.

Applications:

• Engineering and architecture for designing structures.
• Navigation and aviation for flight paths and routes.
• Computer graphics and modeling for rendering three-dimensional objects.
• Physics for analyzing forces and motion in three-dimensional space.

Understanding planes in geometry is essential for various fields, from mathematics and engineering to computer science and beyond. Mastery of plane geometry enables individuals to solve complex problems, visualize spatial relationships, and apply mathematical principles to real-world scenarios.

Conclusion:

Planes are indispensable geometric entities that play a central role in understanding spatial relationships and shapes in geometry and beyond. With their flat, two-dimensional surfaces and infinite extension, planes offer a versatile framework for analyzing geometric concepts, solving problems, and modeling real-world phenomena. Understanding the properties, equations, and applications of planes is essential for mastering geometry and applying geometric principles in various disciplines.